Problems from undergraduate-level olympiads

These olympiads were conducted at the University of Nizhny Novgorod (rus | eng) for undergraduate students. The UNN has three physics departments (the Advanced School of General and Applied Physics, Radiophysics, and Physics), so the students from all three were encouraged to participate. The organization of undergraduate olympiads is not so extensive and systematic as of high-school level.

2006 olympiad in physics, UNN

1. In quiet weather the plane moves in the air with speed v. If there is a wind with a constant speed blowing from point A to point B, the plane covers the way from A to B and back from B to A in time t1. If there is a wind of the same speed in a perpendicular direction, the plane needs time t2 for the same flight. Find the speed of the wind.

2. A uniform magnetic field of induction B is directed parallel to the z axis of the Cartesian coordinate system. At the origin there is a stationary negative charge -Q. A charge q of mass m was placed on the x axis at the coordinate x0 and released with no initial speed. Find the closest distance that the charge may have with the origin.

3. Find the electric field generated by a uniformly charged plate with surface-charge density σ in the gas consisting of an equal number of positive-charge (+q) and negative-charge (-q) particles. The temperature of the gas is T, the energy of thermal motion of the particles is much greater than the energy of interaction with the electric field.

4. A vertical tube of length 2L has the lower end sealed and the upper end open to the atmosphere. The lower half is filled with ideal gas at temperature T0 and the upper half is filled with mercury. The gas is gradually given heat until all mercury spills out. What is the maximum temperature that the gas achieves in this process? The atmospheric pressure is L mm Hg. Neglect surface tension.

5. A flat wave with length λ falls with a certain incident angle on a diffraction grating with spacing d, and the projection of the wave vector on the plane of the grating is parallel to its grooves. Find the minimum angle of incidence when the resulting light has only maxima of order 0.

2000 olympiad in physics, ASGAP, UNN

1. (8 points) Biker races are performed on a narrow circular track. Every biker tries to achieve big speed as faster as possible right after the start. Which part of the circle does he cover before he achieves it?
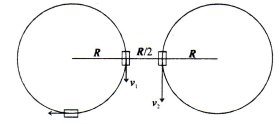	2. (12 points) Cars A and B move on the tracks which are horizontal circles of the same radius lying in the same plane and whose closest points are apart by half the radius. The velocity of car A is v1 = 20 km/h, of car B is v2 = 40 km/h. Find the velocity of car B relative to car A at the moment when they are at the closest points and when car A made a quarter of the revolution after that.
3. (8 points) A little bulb with remaining freon was connected to a large reservoir in which the initial pressure p was twice as big as in the bulb and the temperature was the same as of the outside air. The bulb was disconnected right after being filled up. Find the final (equilibrium) pressure in the bulb if it is not heat-insulated. Neglect the heat exchange with the outside air during filling.
4. (10 points) Inside a big reservoir with helium at temperature T there is a small heat-insulated cavity, in which there is deep vacuum. Find the temperature established in the cavity if a small opening in it, connecting it with the reservoir, is open for a short time.
5. (8 points) Find the magnetic flux through the plane which passes through the open end of a half-infinite solenoid perpendicular to its axis if inside the solenoid far from the open end the magnetic flux in this direction is Φ0.
6. (10 points) A long dielectric cylinder with radius R is polarized electrostatically so that everywhere inside it the polarization P=αr, where α is a positive constant and r is the distance from the axis of symmetry. The cylinder is rotated around its axis with angular speed ω. Find the magnetic induction in the center of the cylinder.
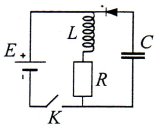	7. (10 points) In the circuit (see figure) the switch K was on for τ=0.1 s. Find the voltage which was established on the capacitor C if the parameters of the circuit are as follows: E=10 V, L=1 H, C=1 μF, R=1 Ω. All elements of the circuit are ideal.
8. (8 points) Pouring milk into the glass you occasionally spilled some of it on the oilcloth, and under the layer of milk you can barely see the pattern of the oilcloth. Considering milk as a mixture of oil balls and water, evaluate the size of such balls.