Nick Kriukov's Website

Problems from high school olympiads

The following olympiads were held at the Radiophysics Department (rus | eng, very outdated) of the University of Nizhny Novgorod, Russia (rus | eng). The competition was at the oblast (regional) level. Generally the oblast-level olympiads admitted high school students (9th - 11th grades in Russian 11-grade school system, 15 - 17 y.o., the difficulty level corresponding to the grade), though 8-graders were allowed to participate as well. Here I have translated the problems from 1996 - 1999 olympiads in which I took part when in secondary/high school. These olympiads take place in the beginning of February every year.

1999 oblast-level olympiad in physics, 11th grade

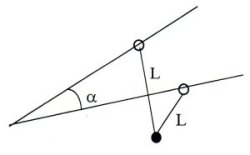	1. (8 points) A hard wire is bent under angle α and placed in a horizontal plane. On the wire there are two identical rings connected by an ideal string of length 2L. In the middle of the string there is a ball attached whose mass is the same as of either ring. At t=0 the rings are held at the same distance from the angle. What should this distance be in order for the rings to have maximum acceleration at the next moment they are released? What is this maximum acceleration?
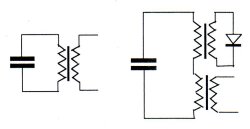	2. (8 points) When a capacitor charged to a certain potential is connected to a transformer with a disconnected secondary winding, the circuit responds with oscillations of period T₀ and amplitude of the current I₀. Plot the current in the primary windings of two such transformers connected in a series to the same capacitor with the same initial charge, versus time. One of the transformers has its secondary winding disconnected, and the other is connected to an ideal diode. The direct resistance of the diode is zero, the opposite is infinity, there is no reciprocal magnetic flux between the transformers.
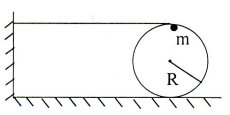	3. (10 points) A frictionless massless cylinder of radius R with a small object of mass m attached to its internal surface is resting on two horizontal tracks. An ideal string is wound around it, one of the ends of it is attached to the cylinder and the other to the wall at the height 2R from the tracks. At the initial moment the string is horizontal, the cylinder is at rest, and the object is at the highest point, infinitesimally inclined clockwise from the vertical. What distance will the center of the cylinder travel by the moment when the tension in the string disappears? Consider that during motion the axis of the cylinder is always parallel to the wall.
4. (14 points) A uniform chain of length 3L and mass m is resting on a pulley so that the hanging parts of it on both sides of the pulley have equal length and the part which is lying on the pulley has length L. There is no friction in the axis of the pulley. Because of an infinitesimal displacement the chain starts moving to the right. What is the force with which it is acting on the pulley when the length of the right end is 3L/2?

1998 oblast-level olympiad in physics, 11th grade

1. (6 points) To decrease the average power emitting on a lamp in an AC circuit, a diode was connected to it in a series. The direct resistance of the diode is much less than that of the lamp, and the opposite resistance is equal to the one of the lamp. How did the average (on the period) power emitting on the lamp change? (Calculate the ratio of it over the original power.)
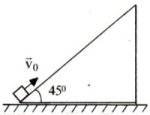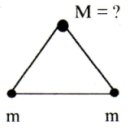
	2. (10 points) A small cube was pushed up the inclined surface of the wedge with speed v₀. The base angle of the wedge is 45°, the masses of the cube and the wedge are equal, all surfaces are frictionless. Find the minimum radius of curvature of the cube's trajectory in the stationary frame of reference. The cube does not reach the top of the wedge.
	3. (12 points) A piece of ice on the spring attached to a wall oscillates on a frictionless surface. Because of melting the mass of the ice decreased by half. How did the amplitude of oscillations change? Consider that the melting is slow and the water produced by melting does not influence the oscillation.
	4. (12 points) Three balls whose electric charges are equal are bound to one another by strings of equal length and are resting on a smooth horizontal surface. The masses of two of them are the same and equal m. The string connecting these two balls is then eliminated. Which values of mass M of the third ball are necessary so that the speeds of the balls with mass m will be maximum at the moment when all three balls are on a straight line?

1998 oblast-level olympiad in physics, 10th grade

1. (6 points) What is the highest point of a stone thrown vertically upward if the time in flight was 4 s and during the last second it covered half the total way? Neglect air resistance.
	2. (10 points) A small cube was pushed up the inclined surface of the wedge with speed v₀. The base angle of the wedge is α, the masses of the cube and the wedge are equal, all surfaces are frictionless. Find the radius of curvature of the cube's trajectory at the highest point in the stationary frame of reference. The cube does not reach the top of the wedge.
3. (12 points) A puck of mass m₁ was given initial speed v₀ along a board of mass m₂ which had before been resting on the water surface of the lake. After going distance s along the board, the puck stopped. Find the work of dry friction forces between the puck and the board if it is known that the maximum speed of the board was v and the force of viscous friction between the board and the water is proportional to the speed of the board, and the coefficient of proportionality is k.
4. (12 points) An isolated cylindrical vessel is divided in two parts by a light piston which can slightly conduct heat and can freely move along the vessel. In one part of the vessel there is 10 g of helium at temperature 500 K, and in the other one 3 g of hydrogen at 400 K. What will the temperature be in the vessel after equilibrium is established? (4 points) What is the ratio of the final and initial pressure? (4 points) What is the heat capacitance of each gas in the beginning? (4 points) Neglest the heat capacitance of the piston and walls of the vessel.

1998 oblast-level olympiad in physics, 9th grade

1. (6 points) What is the highest point of a stone thrown vertically upward if the time in flight was 4 s and during the last second it covered half the total way? Neglect air resistance.
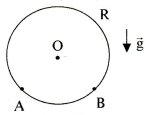	2. (8 points) A small ball is bouncing inside of a smooth stationary sphere of radius R, hitting the surface elastically at symmetric points A and B. Find the minimum speed of the ball in this process if its trajectory goes through the center O.
3. (12 points) In the bottom of a cylindric vessel with thin walls and an open top there is a narrow passage. When it was placed on the water surface, it immediately went half-height under water, and then sank in 2 min as a result of slow flow of the water through the passage. What time will be required to sink for a vessel of the same size and with the same passage, but made of a material whose density is three times less? Consider that the rate of water flow through the passage is proportional to the pressure difference at its ends, and the vessels are oriented vertically at all times.
	4. (14 points) A small cube was pushed up the inclined surface of the wedge with speed v₀. The base angle of the wedge is α, the masses of the cube and the wedge are equal, all surfaces are frictionless. In what time will the cube return to the initial point on the surface of the wedge?

1997 oblast-level olympiad in physics, 9th grade

1. (6 points) A car which was slowing down with a constant acceleration covered the distances AB and BC of 51 m and 24 m during the times 3 s and 2 s respectively. What distance will it cover from point C until it stops?
2. (10 points) Two cyclists departed at the same time; one from point A to point B, the other from B to A. They met at the point 8 km from point A and proceeded. Each of them, upon arriving at the destination, turned around and went back. On the way back they met again. Find all possible values of the distance from B to the place where they met again. The speeds of the cyclists stay constant all the way.
3. (12 points) In the cylindrical vessel with cross-section area S there is water and a piece of ice, both at 0°C. There is a string frozen into the ice, whose other end is attached to the bottom of the vessel. As a result of heat taken out the mass of the ice increased twofold. By what value Δh can the level of the water in the vessel change (find the maximum and minimum possible values of Δh)? The ice does not touch the walls or bottom of the vessel. The densities of water ρ₀ and ice ρ are known.
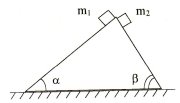	4. (12 points) A massless wedge with base angles α and β is resting on a smooth horizontal table. Two small objects start sliding simultaneously from the top of the wedge. What ratio of their masses m₂/m₁ is necessary for them to reach the surface of the table simultaneously?

1996 oblast-level olympiad in physics, 9th grade

1. (6 points) An object is thrown with angle α to the horizontal with initial speed v₀. After what time its velocity vector will turn 90° from the initial position? Neglect air resistance.
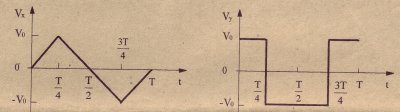
2. (10 points) The particle moves in the plane x, y. The projections of its velocity on the axes x, y are changing with time as in the figure. Plot the trajectory of the particle. Find the radius of curvature of the trajectory of the particle at t=T/2. At t=0 the particle was at the origin.
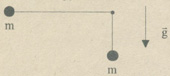	3. (14 points) Two balls of the same mass m are attached to the ends of a light rod which is bent in the right angle. The horizontal axis of rotation is going through the vertex, one part is twice as long as the other. The system is held at the position as shown in the figure, and then released. Find the force with which the rod acts on the axis of rotation at the moment it was released.
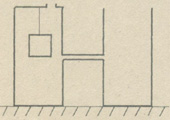	4. (10 points) Two identical cylindrical vessels are connected with a tube at half height. The left vessel is covered, with a small hole being in the cover. The cross section area of each cylinder is 0.03 m², their height is 0.4 m. A wooden cube with side length 0.1 m is suspended from the cover of the left vessel. The bottom face of the cube is at the level of the tube. The right vessel at t=0 starts receiving water with a constant rate of 0.001 m³/min. Plot the pressure on the bottom of the right vessel versus time. The density of water is 1000 kg/m³, the density of wood is 600 kg/m³. Ignore atmospheric pressure.