Graphics & Media Lab. >> Курсы >> Курс Шикина 2000г.
Ниже приводится простейшая реализация кубика. По мере работы мы будем добавлять
этому объекту новые методы.
////////////// simple geometric structures ////////////////
struct Edge
{
int v1, v2; // vertices indexes
int f1, f2; // facet's indexes
};
struct Facet
{
int v [4]; // vertices indexes
Vector3D n; // normal
};
/////////// object-oriented model of unit cube /////////////
class Cube
{
public:
Vector3D vertices [8];
Edge edges [12];
Facet facets [6];
Cube ();
void initEdge ( int i, int v1, int v2, int f1, int f2 )
{
edges [i].v1 = v1;
edges [i].v2 = v2;
edges [i].f1 = f1;
edges [i].f2 = f2;
}
void initFacet ( int i, int v1, int v2, int v3, int v4 )
{
facets [i].v [0] = v1;
facets [i].v [1] = v2;
facets [i].v [2] = v3;
facets [i].v [3] = v4;
}
void computeNormals ();
void applyTransform ( const Vector3D&, const Matrix3D& );
};
//////////////////// Cube methods ////////////////////
Cube :: Cube ()
{
// 1. init vertices
for ( int i = 0; i < 8; i++ )
{
vertices [i].x = i & 1 ? 1.0 : 0.0;
vertices [i].y = i & 2 ? 1.0 : 0.0;
vertices [i].z = i & 4 ? 1.0 : 0.0;
}
// 2. init edges
initEdge ( 0, 0, 1, 2, 4 );
initEdge ( 1, 1, 3, 1, 4 );
initEdge ( 2, 3, 2, 3, 4 );
initEdge ( 3, 2, 0, 0, 4 );
initEdge ( 4, 4, 5, 2, 5 );
initEdge ( 5, 5, 7, 1, 5 );
initEdge ( 6, 7, 6, 3, 5 );
initEdge ( 7, 6, 4, 0, 5 );
initEdge ( 8, 0, 4, 0, 2 );
initEdge ( 9, 1, 5, 1, 2 );
initEdge ( 10, 3, 7, 1, 3 );
initEdge ( 11, 2, 6, 0, 3 );
// 3. init facets
initFacet ( 0, 4, 6, 2, 0 );
initFacet ( 1, 1, 3, 7, 5 );
initFacet ( 2, 0, 1, 5, 4 );
initFacet ( 3, 6, 7, 3, 2 );
initFacet ( 4, 2, 3, 1, 0 );
initFacet ( 5, 4, 5, 7, 6 );
}
void Cube :: computeNormals ()
{
for ( int i = 0; i < 6; i++ )
facets [i].n = (vertices [facets [i].v [1]] -
vertices [facets [i].v [0]]) ^
(vertices [facets [i].v [2]] -
vertices [facets [i].v [1]]);
}
void Cube :: applyTransform ( const Vector3D& translation,
const Matrix3D& transform )
{
for ( int i = 0; i < 8; i++ )
vertices [i] = translation + transform * vertices [i];
}
Для простоты все переменные и методы это класса сделаны общедоступными (в
серьезных проектах этого, конечно, следует избегать). В конструкторе инициализируется
единичный куб, расположенный углом в начале координат. Метод computeNormals
вычисляет единичные вектора внешней нормали для каждой грани (когда мы подвергаем куб
преобразованию, то вектора нормали не преобразуются и требуют перевычисления). Метод
applyTransform подвергает куб линейному преобразованию общего вида, задаваемого
матрицей преобразования и вектором сдвига (напомним, что сдвиг в трехмерном
пространстве нельзя представить при помощи матрицы третьего порядка) по следующей
формуле
v' = translation + transform*v.
Еще одним классом, которые нам понадобится, является камера - объект, который
будет осуществлять перспективное преобразование из трехмерного пространства, где
расположен куб (объектное пространство) в пространство экрана (картинную плоскость).
Делается это в два этапа: на первом шаге осуществляется преобразование из трехмерного
объектного пространства в трехмерное пространство камеры по формуле:
v' = M (v-pos) ,
а на втором шаге выполняется классическое перспективное проектирование по формулам
X = x / z,
Y = y / z .
К комбинации двух таких преобразований может быть сведено любое перспективное
преобразование. Преобразование, используемое на втором шаге, является классическим и
достаточно хорошо объяснено в различных учебных пособиях. Остановимся на первом
преобразование и на том, откуда берутся соответствующие матрица и вектор более подробно.
Как несложно убедится, вектор pos является той самой точкой, в которой находится сама
камера. С матрицей М дело обстоит сложнее. Посмотрим, каким способом пользователю
удобнее всего задавать камеру. Прежде всего он должен задать местоположение камеры р и
точку, в которую камера должна смотреть lookAt. Камера может находится в заданной точке
и смотреть в заданном направлении, но быть повернутой на произвольный угол вокруг
прямой, проходящей через эти две точки. Поэтому необходимо задать еще и ориентацию
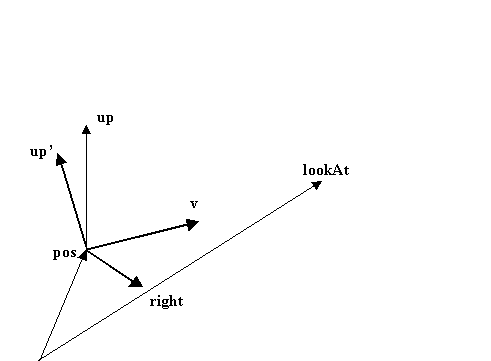
камеры. Удобнее всего это сделать, задав дополнительный вектор up, направленный вверх.
Посмотри теперь, как по этим трем векторам строится матрица М.
Прежде всего построим вектор v, задающий направление "взгляда" камеры:
v = lookAt - p.
Следующий шаг - ортогонализация ветора v вектору up. Для этого вектор up, преобразуется
так

Где

Чтобы найти третий вектор, соответствующий направлению вправо, воспользуемся
векторным произведением right = [ up,v ]
Исходный текст объекта Camera приводится ниже:
#ifndef __CAMERA__
#define __CAMERA__
#include "Point.h"
#include "Matrix3D.h"
class Camera
{
public:
Vector3D pos; // camera position
Matrix3D transf; // camera transform (from world to camera space)
Camera ( const Vector3D& p, const Matrix3D& t )
{
pos = p;
transf = t;
}
Camera ( const Vector3D& p, const Vector3D& lookAt,
const Vector3D& up,
float xScale, float yScale );
void project ( const Vector3D&, Point& ) const;
};
#endif
#include "Camera.h"
Camera :: Camera ( const Vector3D& p, const Vector3D& lookAt,
const Vector3D& up,
float xScale, float yScale )
{
Vector3D v = lookAt - (pos = p); // direction of view
float a = -(up & v) / (v & v);
Vector3D up1 = up + a * v; // orthonormalize up and v
Vector3D right = up ^ v;
up.normalize () *= yScale;
right.normalize () *= xScale;
v.normalize ();
transf [0][0] = right [0];
transf [0][1] = right [1];
transf [0][2] = right [2] + xScale / 2; // move (0,0,z) to center
transf [1][0] = up [0];
transf [1][1] = up [1];
transf [1][2] = up [2] + yScale / 2; // move (0,0,z) to center
transf [2][0] = v [0];
transf [2][1] = v [1];
transf [2][2] = v [2];
}
void Camera :: project ( const Vector3D& v, Point& p ) const
{
Vector3D vt = transf * (v - pos);
p.x = (int)(vt.x / vt.z);
p.y = (int)(vt.y / vt.z );
}
Первым шагом в визуализации куба будет построение простого каркасного изображения. Для
этого проектируем все вершины куба и выводим все ребра, составляющие куб.
void Cube :: drawWireframe ()
{
Point p [8];
// project vertices
for ( int i = 0; i < 8; i++ )
camera.project ( vertices [i], p [i] );
computeNormals ();
// draw all faces
setcolor ( WHITE );
for ( i = 0; i < 12; i++ )
line ( p [edges [i].v1].x, p [edges [i].v1].y,
p [edges [i].v2].x, p [edges [i].v2].y );
}
main ()
{
Cube cube;
int drv = VGA;
int mode = VGAMED;
cube.applyTransform ( Vector3D ( -0.5, -0.5, -0.5 ),
rotateX (M_PI / 6) * rotateZ ( M_PI / 6) );
initgraph ( &drv, &mode, "" );
cube.drawWireframe ();
getch ();
closegraph ();
}
Все исходные тексты можно взять здесь.
Graphics & Media Lab. >> Библиотека | Курсы | Графикон



